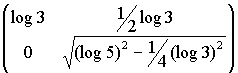transforming the lattice:A reaction from Paul Erlich about my 'expressibility' measure made me think about the relation of these measures and the orientation of a lattice.
Now the 'translation' from an equidistant lattice to Paul's triangular lattice can be accomplished with a matrix like this:
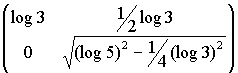transforming the lattice:
to
The contour of a complete block within a certain limit of my measure looks like:
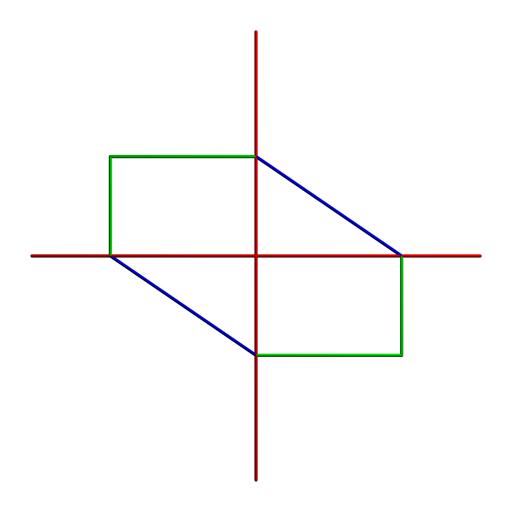
and after Paul's transformation like this:
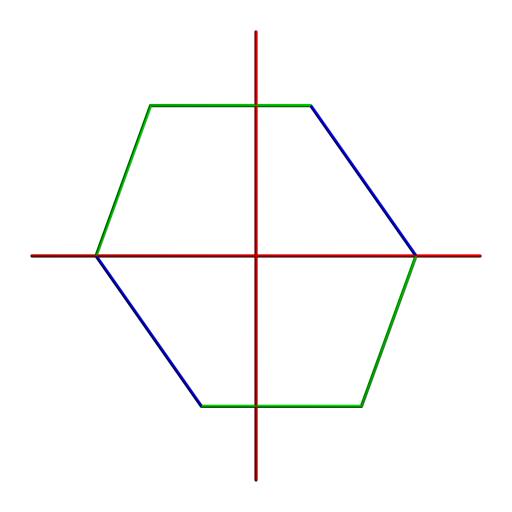
So indeed, it's still a skewed shape, indicating the discrepancy with Paul's measure.
To create a symmetrical hexagon we would need the transformation matrix:
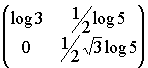which would result in:
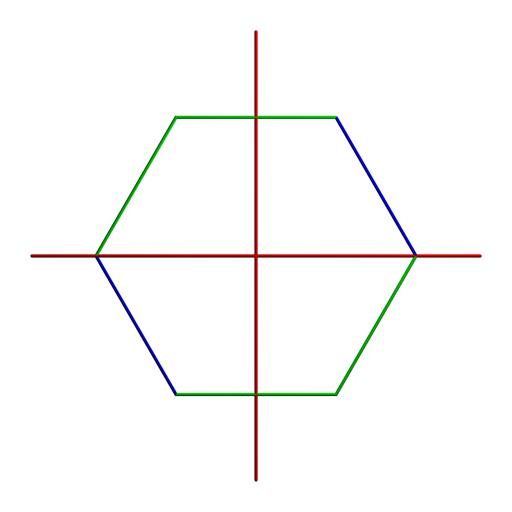
A lattice after this transform would look like:
Now we seem to hit a paradox, because the measure of a 5/4 (blue) and a 5/3 (green) should be the same, just as
in Paul's isosceles triangle case. This is caused by the fact that the boundary of my block should be tranformed
to a circle, not a regular hexagon. Performing such a transform will make the lattice look like:
Of course, since this is a non-linear transform, this only represents the metric relative to the center, not necessarily
from any other point in the lattice.